. These are the black notes on the piano and make up the full complement of twelve notes used in Western music.BBC Micro Music Masterclass
If you stop to consider the matter you will realise that literally every subject of any complexity inevitably acquires its own specialist vocabulary. Music is no exception to this general rule for just as the pioneers discovered that it was necessary to develop languages like BASIC and FORTH to facilitate the use and development of computer technology, so the world of music also has a special language all of its own. Since the scope of music only encompasses pitched notes and rhythm, however, its structure is considerably simpler than that of any computer language. For this reason I believe that most newcomers to music theory who have had some general computer experience will pick up the rudiments of music theory quite easily.
I have felt it necessary to digress somewhat and emphasize this point because of the experience of music teaching many of you will doubtlessly have had at school. For me, school music lessons comprised of note learning, primarily concerned with absorbing key signatures, composers’ names and other pieces of musical gobbledygook. In this chapter I do not intend to bombard you with meaningless nmemonics designed to make it easier for you to remember the notes of the treble clef. This type of knowledge can be acquired quite naturally through growing familiarity with music itself. Instead, I intend to provide you with a vocabulary which will allow you to understand the more musically technical sections of this book and, show you how easy it is to use sheet music as reference material.
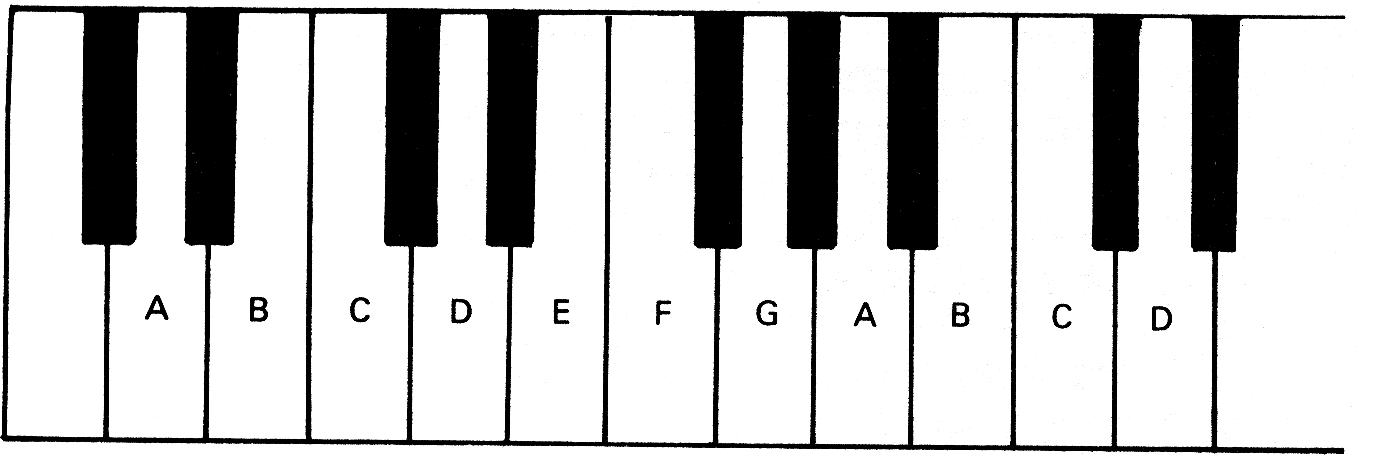
In order to make it possible for us to speak about individual note pitches we must first start off by giving each note a name. The accepted method for doing this is to call them after the letters in the alphabet between A and G. If you look at a piano keyboard, you will see that the notes are found at the positions shown below:
On the BBC Micro we have pitch values such that the A note above Middle C=89, B=97, C=101, D=109, E=117, F=121, G=129 and, for the A note one octave above the first, A=137. As you can see, this method of notation has its drawbacks. All the As, in whatever octave, have the same name. Bear in mind that a note which is one octave above another has double that note’s frequency.
A better method for illustrating pitch is to abandon numbers and letters altogether and draw them on a musical stave, as is illustrated below:
In this case there is no ambiguity in discriminating between notes of different octaves. In addition, the concept of higher notes being situated higher up the stave is both extremely helpful and logical. A stave is, of course, the name given to the standard arrangement of five lines!
The symbol at the beginning of the stave is called a Treble Clef. This clef is used for the treble register of a piano and all instruments that play in that range, such as flutes, oboes, guitars etc. Bass instruments have their own clef, unsurprisingly called the Bass Clef. This is used by instruments such as trombones, bassoons and double basses. It looks like this:
A piano covers such a large range that it uses both clefs, and we can correlate piano keyboard and notation as follows, with each white note having its own line or space. BBC Micro pitch values are shown also.
The above diagram includes extra notes which are either a semitone higher (sharp) or lower (flat) to the white notes. The sharp sign is # and the flat sign . These are the black notes on the piano and make up the full complement of twelve notes used in Western music.
It is worth pointing out at this juncture that the rules and notations described in this chapter apply only to Western music. If we were playing Indian music, for instance, a completely different set of rules would apply. This is analogous to the use of different languages in computers for while the vocabulary itself might seem to be different, the general principles which apply are, of course, the same.
The only other area you need to know about before you are ready to read and write musical pitches concerns key signatures and keys. Different keys arise because of the particular tone intervals used in Western scales. An interval is the pitch difference between any two notes. Turning back to the piano keyboard, you, will see that if you play two adjacent notes, ie.: C to C or E to F, the interval would be one semitone. This is the smallest interval possible in Western music.
There are twelve semitones in every octave, but as most of you will know the scales normally used only use eight of these notes. For example, the scale of C Major comprises of the notes:
C D E F G A B C
This is because the intervals between the notes of a Major scale always conform to a particular pattern:
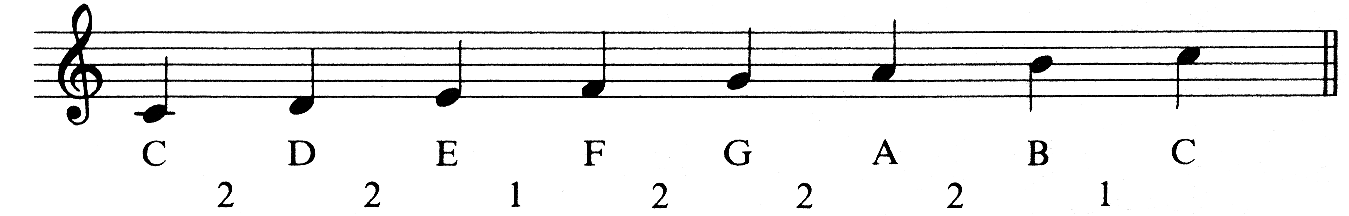
Where a 2 indicates 2 semitones or one full tone difference and 1 shows a 1 semitone change between the notes. As you can probably guess, if you start your scale on a note other than C, say F#, it would be necessary to play some black notes on the piano and include some sharps or flats in the notation of the scale.
Let us look at the scale of F#, which would be:
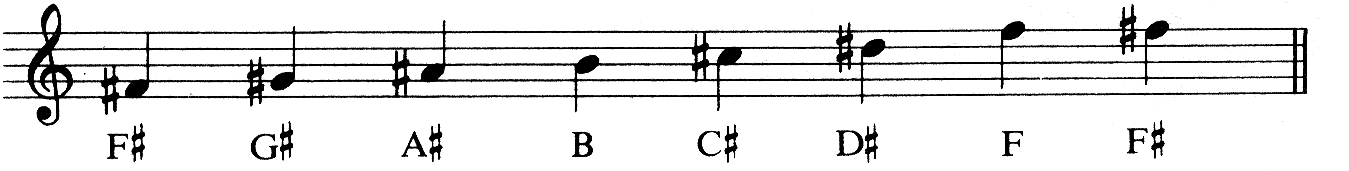
You have probably guessed that it would prove rather tedious writing sharps every time they occurred in F # Major so they are written on the stave just once, at the beginning of the piece of music to be played in that key, as follows:
This is called the key signature and each of the twelve possible scales (count them!) has its own unique signature.
Should we need a note which is not to be played sharp or flat as required by the Key signature it has a natural sign,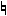 
, placed before it. This effect lasts for a bar, and if the same note reverts to the key it requires a sharp or flat sign to signify this.
You will no doubt be gratified to learn that you are now equipped with enough information to take a piece of sheet music and convert the musical notation into pitch information for the computer - and vice versa! Alternatively, you could write a program to do the job for you, but you would be well advised to wait until you’ve availed yourself of the techniques still to come!
DURATION NOTATION
The use of the stave form of musical notation really comes into its own when dealing with durations. Various symbols are used to indicate the length of a note. These are as follows:
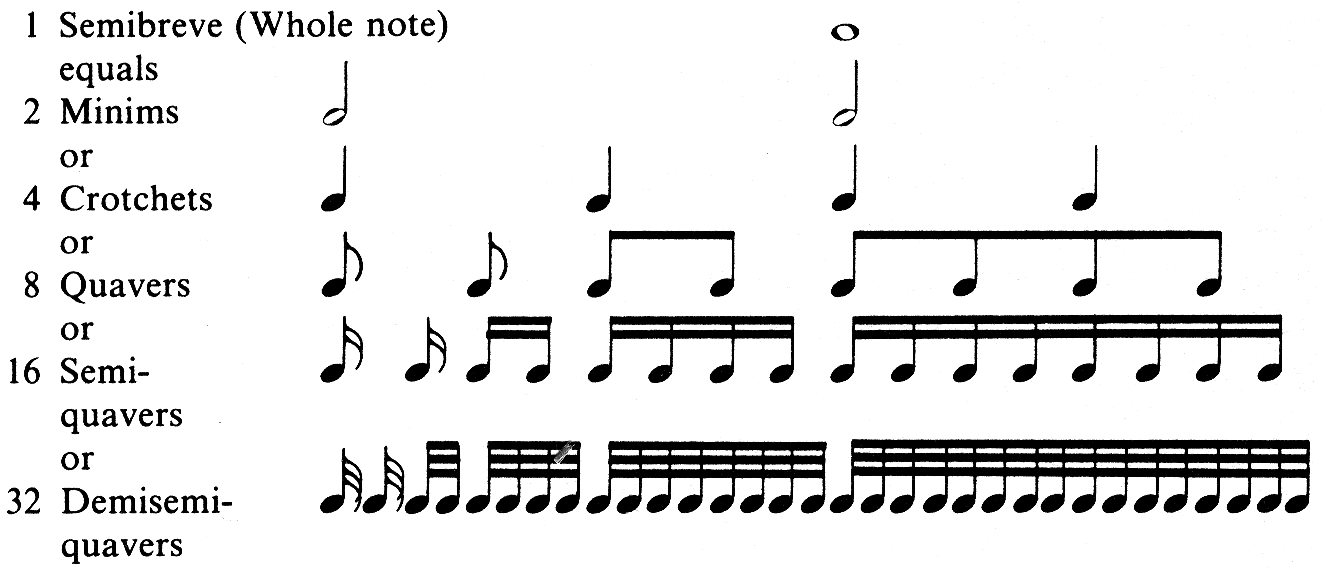
A dot after a note increases its value by half, so that 
is equivalent to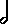 
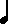
These note lengths are defined relative to each other, and are completely independent from the tempo or speed of the music, which defines the length of a bar (see below). Each note duration symbol has it equivalent note rest symbol, which is used to mark the periods of silence which fall between notes:
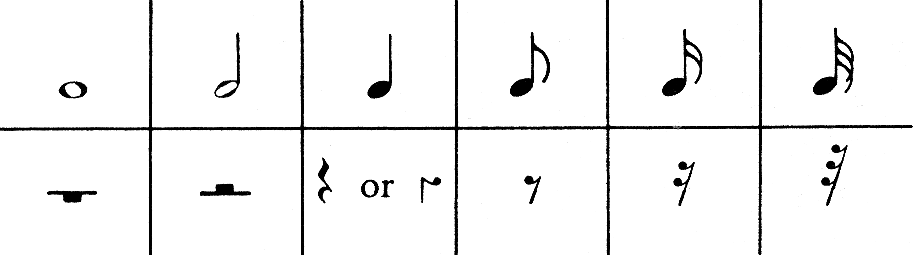
It would of course be perfectly possible simply to string crotchets and quavers in a line across the page, with the only breaks in the line consequently being the ends of pages. This would, however, prove rather confusing, don’t you agree! One better way of dealing with this problem would be to group them in easy-to-cope-with bundles, rather like stringing words together within a sentence. The musical name for one of these bundles is a Bar and the length of each bar is given by the time signature. The time signature is written at the beginning of a piece of music, directly after the key signature:
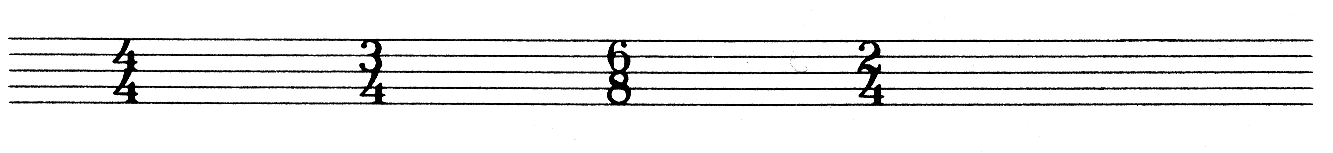
The upper figure is the number of beats per bar length and the lower figure gives the length of each beat. Hence 3/4 indicates three beats per bar with each beat a quarter note, i.e. a crotchet. 6/8 would indicate six beats per bar with each beat an eighth note, i.e. six quavers per bar. The most common time signatures you will encounter are 4/4 (four crotchets per bar) and 3/4, waltz time.
All that now remains to be added to this body of information is the final piece which is required to define that rhythm of a tune. And that is the tempo. Tempo is normally given in terms of crotchets per minute. So
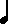=120 would mean 120 beats per minutes. If you look at classical music, you will notice that various Italian words are used to indicate the overall tempo of a piece. A selection of the commonly encountered terms are listed below.
Classical Tempo Terms Adagio Slow, leisurely Allegro Lively, reasonably fast Andante Moderate pace Grave Very slow Largo Slow and stately Lento Slowly Presto Very quick Prestissimo As fast as possible Vivace Quick
When programming music on the BBC tempos can be converted into time values by using the updated Metronome program which follows below. You will notice that I use the words ‘time values’ and not ‘duration’ in this case. As I mentioned earlier, this is because the duration parameter’s 1/20th of a second resolution is not great enough to provide for the full range of possible tempos. For instance, if a tempo of 120bpm is required, then there is no problem. That is to say 120bpm=2bps or 10 (20/10) duration values for a crotchet. However, if, say, we wanted a tempo of 119bpm this would give 1.95bps or 20/1.95=10.256... duration values.
The BBC would round this non-integer value down to ten, which would produce a tempo of 120bpm just as before. The next slower usable tempo is 100, for a crotchet value of 12. Not only would this be true, but even at 120bpm quavers are the shortest notes allowed. Semiquavers would give a D value of 2.5, which is also unacceptable. Refer to the table given on page 22.
Let us now get back to Metronome, shall we? The first thing we notice is that this means an alternative method for inputting timing must be found. One possible available method is to use the TIME variable. By controlling the length of a REPEAT... UNTIL loop of the type:
TIME=0: REPEAT:UNTIL TIME < length%
we could resolve our timing down to around 1/100th of a second. It must be noted that for certain applications this is still not fine enough, however.
Another method would be to resort to a machine code routine. The simplest and most effective BASIC method available is to use a FOR... NEXT loop, however, as is done here:
the rest of this chapter I should like to turn to the consideration of some of the more useful musical ideas that have been developed over the past few hundred years. Let us start this quest by seeing how musicians gradually came to assemble notes into scales and arpeggios.
SCALES AND ARPEGGIOS
As Western music gradually developed over the centuries it was found that of the twelve possible notes (including sharps and flats) some were used more than others. Initially this was because crumhorns, bagpipes and the like were only capable of playing certain notes of the scales. It was left to Bach to devise a system whereby the scales of all the instruments played in his day were incorporated into one ‘even-tempered’ scale called the chromatic scales.
With the arrival of the chromatic scale any number of scales (sequences of notes) could henceforth be derived. The most common of these is the Major scale, as illustrated previously. The importance of the scale lies in establishing a note priority. In the key of C Major any note from the scale will sound more ‘in tune’ than any note outside it. Older forms of music such as that popularized by Bach, as well as fledgling jazz, seldom if ever strayed to notes outside the scale in use. More modern forms, such as bebop or music of composers like Bartok, on the other hand, positively revel in the use of ‘outside’ notes. Either way, it goes without saying that the scale is still an invaluable melodic framework.
Other scales commonly used in various forms of music are the Harmonic and Melodic Minor, the Natural Minor, Blues and the primitive Pentatonic. In addition to scales, a second level of note priority is provided by arpeggios, so let us now turn to survey precisely what is meant by the term.
An arpeggio, in its basic form, is a broken chord made up of the 1st, 3rd and 5th notes of whatever scale happens to be in use. For instance, this sequence would make the arpeggio of C Major:
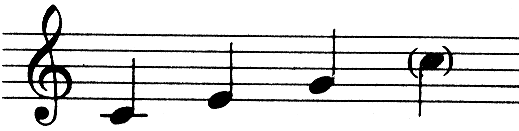
generating accompaniment by supplying notes which can be played simul-taneously with the melody notes. For an example, see the “Happy Birthday” program in the previous chapter. A chord sequence is the name given to the order in which the chords are played underneath any given melody. Because of the importance of the chord sequence in defining a harmonic accompaniment a method of notating chords had to be developed over the centuries. The basic chord symbol defines the note triad (three note chord) to be used. Look at the table below to see what I mean:
C... C,E,G 1st, 3rd and 5th notes of the C Major scale A... A,C,E 1st, 3rd and 5th notes of the A Major scale Dm... D,F,A 1st, 3rd and 5th notes of the D Minor scale
In these cases the lack of a subscript indicates a Major chord. A small m indicates a Minor chord. There are various other symbols which you also might come across, including Dim, which indicates the 1st, 3rd and 5th of a diminished scale, and Aug, which indicates a Major chord with an augmented 5th note, i.e. the 5th is made a semitone sharper than it would be otherwise.
A number of additional notes can be added to the basic three-note chord if you wish to make 4,5 or even 6 note chords. Using the key of C, here are some examples:
Name Added Notes Notes Chord MAJ7 7th note of Major scale CEGB CMAJ7 7 Minor 7th note CEGB C7 6 6th note of Major scale CEGA C6 9 9th+Minor 7th notes CEGB D C9 11 11th+9th+7 CEGB DF C11
These symbols are then written above the part of the melody to which they apply. This can be seen if you look at most sheet music, as well as examples scattered throughout the pages of this book.
You will doubtlessly remember me saying earlier on in the text that melodies suggest particular chord sequences; it is equally true to say that chord sequences also suggest certain melodies. Melodies could be generated by describing a chord sequence and letting the computer generate rhythms and melodies. This can be accomplished using a constrained random numbers generator, the constraints, in their most basic form, being the harmonic considerations mentioned above. Further constraints which would also need to be considered would include song or piece structure and rhythm.
MUSICAL STYLES
Rhythm, or lack of it, is very important in determining the impact of a particular piece of music. Most of the popular styles of music, such as pop, folk and jazz, embrace and are distinguished by their strong and distinctive rhythms. More esoteric forms of classical music, however, are slightly less simple to pin down. We will therefore limit our discussion to general points of style and structure and go into more detail about specific areas in the chapter which concentrates on pinning down and therefore explaining automatic composition.
Virtually every form of music you can think of relies on and uses a certain amount of repetition as a structural device. If you think of the popular children’s song, ‘Frere Jacques’, for example, you will see how this device makes it possible to reinforce and emphasise themes by creating memorable refrains.
FRERE JACQUES
You will notice that this melody has a total of eight bars. Each bar contains a distinct phrase, and these phrases appear in the pattern AA BB CC DD, i.e. the first bar is played, and is then repeated. a new phrase is introduced in the third bar, then this is repeated - and so on.
While this may not be a particularly common type of structure, it does provide us with a very clear example, since each phrase is repeated exactly. It is, however, more common to have slightly different endings to each phrase.
The structures A A B A or sometimes A A B C are frequently encountered. The latter is a frequently used structure both in classical pieces and in popular songs. In this case, first the main theme is stated (this could be of any length and is usually eight bars in the case of songs) and then the theme is repeated. Sometimes it incorporates a variant ending which leads the song into the new theme (or middle eight, in the case of song structure). At the end of the middle eight either of two possibilities is open to the composer: In classical music, the most common option is the recapitulation of the original theme; in the case of the song either a recapitulation or the introduction of an ending-theme are equally common.
One device commonly used in composing both folk and pop music is to include a verse of eight or sixteen bars followed by a chorus. The purpose of the verse is to relate the song’s narrative, and the chorus usually contains a simple, memorable ‘hook’ line which the audience can easily remember. This type of structure can still be used even when no words are being sung. The following original piece employs the verse/chorus format:
Another common musical form is known as the twelve-bar blues. This form employs what could be described as an A A B structure. The main theme is played, then repeated, after which a concluding theme is played. In this example the chords which are played are changed in a traditional sequence, as is illustrated below for the key of C:
C/// C/// C/// C/// F/// F/// C/// C/// G/// F/// C/// C///
Let us leave this topic for the moment, since blues and various other types and styles of music can be explored in greater depth when we come to apply some of our new-found musical knowledge to programming and BBC Micro. In the chapters which follow we shall also attempt to draw musical symbols and staves, generate random music in particular styles, interface the BBC with synthesisers and program from sheet music. Hopefully, on the basis of the expertise we have so effortlessly accumulated in this chapter, none of these tasks will prove insurmountable, and all will enhance our musical enjoyment and output.